非透视投影变换
非透视投影包括 R(旋转)、S(缩放)、T(位移)、虚拟摄像机变换、正视投影变换,所有的非透视投影变换 都是 R S T 组合而来的
位移变换
假设我们有一个向量代表一个物体 V=(x,y) ,然后我们想平移它
比如这样:V′=(x+tx,y+tx)
而矩阵运算
[acbd]⋅[xy]=[ax+bycx+dy]
没有办法出现常数,所以我们就可以增加一个维度:
$\begin{bmatrix}
x\
y\
1
\end{bmatrix} $
然后再使用一个 3×3 的矩阵来做变换
⎣⎢⎡x′y′1⎦⎥⎤=⎣⎢⎡100010txty1⎦⎥⎤⎣⎢⎡xy1⎦⎥⎤=⎣⎢⎡x+txy+tx1⎦⎥⎤
得到 x′=x+xt , y′=y+yt
这样我们就可以完成位移了,这个吧多出来的维度就叫齐次坐标。
同样我们统一使用齐次坐标来进行缩放和旋转,因为这样就可以一直保持向量是多一个维度的(也就是多出来的那个齐次坐标),直接相乘不用来回增减齐次坐标了。
T=⎣⎢⎡100010txty1⎦⎥⎤
缩放变换
S=⎣⎢⎡sx000sy0001⎦⎥⎤
旋转变换
R=⎣⎢⎡cosθsinθ0−sinθcosθ0001⎦⎥⎤
三维物体变换
位移
T=⎣⎢⎢⎢⎡100001000010txtytz1⎦⎥⎥⎥⎤
缩放
S=⎣⎢⎢⎢⎡sx0000sy0000sz00001⎦⎥⎥⎥⎤
旋转
Rx=⎣⎢⎢⎢⎡cosθsinθ00−sinθcosθ0000100001⎦⎥⎥⎥⎤
Ry=⎣⎢⎢⎢⎡cosθ0sinθ00100−sinθ0cosθ00001⎦⎥⎥⎥⎤
Rz=⎣⎢⎢⎢⎡10000cosθsinθ00−sinθcosθ00001⎦⎥⎥⎥⎤
透视投影变换
小孔成像
透视投影变换能够呈现出近大远小透视效果,更符合我们的视觉感受
透视投影模拟的是针孔摄像机,或者说小孔成像
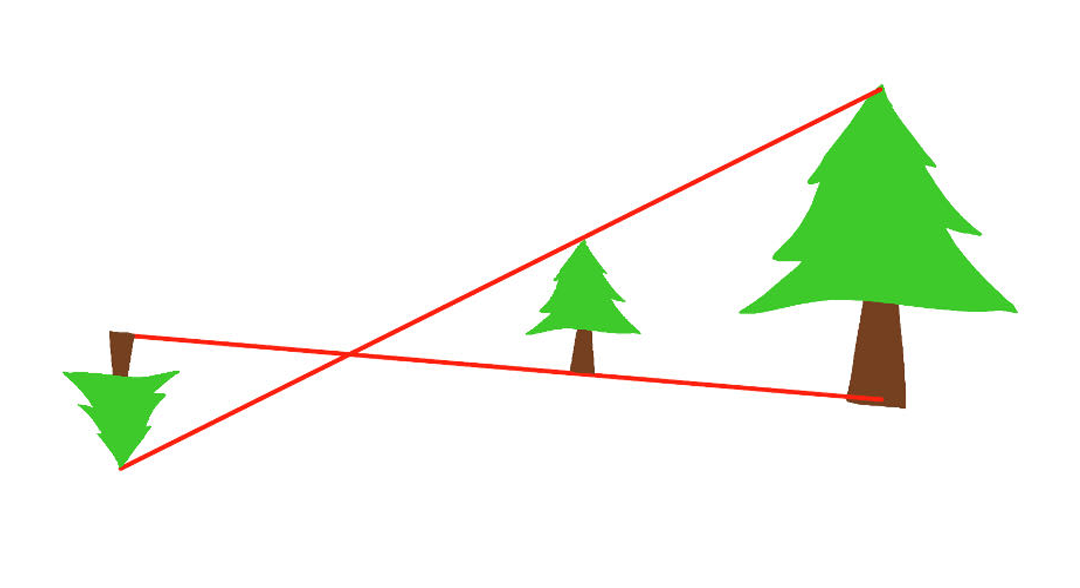
小孔成像会在黑盒里的真空后面后面呈现一个倒立的图像,但是我们在计算机里可以将图像放在小孔前面,这样不仅可以避免图像颠倒,写代码的时候还会更直观
而且这个小孔的位置就可以成为我们的观察点
矩阵计算
然后我们就可以计算一下这个最终呈现的像的大小
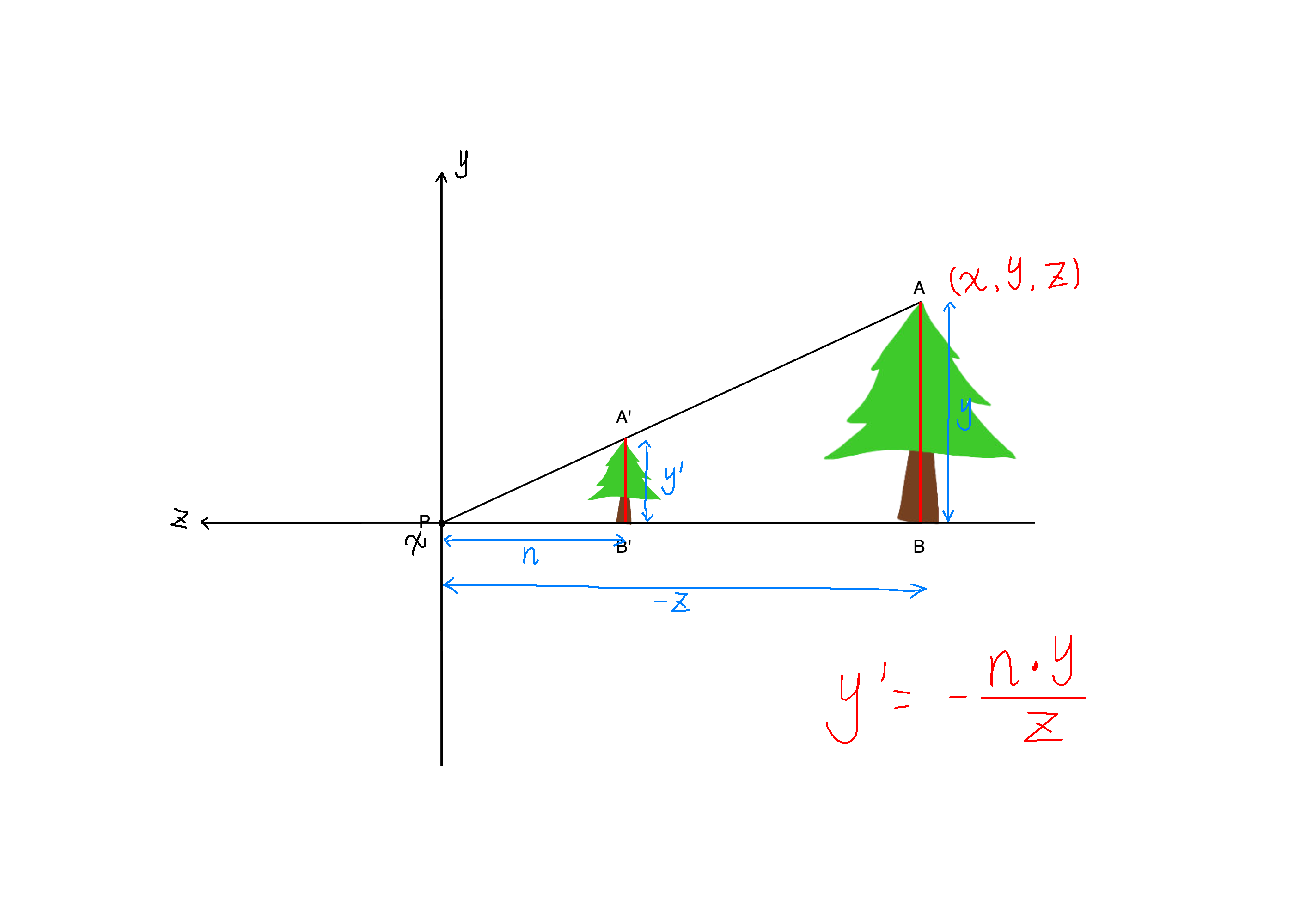
如图所示,我们用相似可以简单推出 y′=−zn⋅y ( py=−z 是因为坐标 z 是 A 点的 z 轴坐标)
成像的 y′ 与 z 成反比,正好符合近大远小的规律
然而,矩阵运算是乘法和加法,没法很方便地计算除法
所以我们这里使用齐次坐标
⎣⎢⎡AEIBFJCGK⎦⎥⎤⋅⎣⎢⎡xyz⎦⎥⎤=⎣⎢⎡Ax+By+CzEx+Fy+GzIx+Jy+Kz⎦⎥⎤
最终将得到的向量除以 z 分量得到:
⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡Ix+Jy+KzAx+By+CzIx+Jy+KzEx+Fy+Gz1⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤
就得到了最终的答案,在成像位置不变的时候,z 越小显示的图像越大,反之越小,三维物体也是同样的道理:
⎣⎢⎢⎢⎡AEIMBFJNCGKODHLP⎦⎥⎥⎥⎤⋅⎣⎢⎢⎢⎡xyzw⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡Ax+By+Cz+DwEx+Fy+Gz+HwIx+Jy+Kz+LwMx+Ny+Oz+Pw⎦⎥⎥⎥⎤
归一化:
⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡Mx+Ny+Oz+PwAx+By+Cz+DwMx+Ny+Oz+PwEx+Fy+Gz+HwMx+Ny+Oz+PwIx+Jy+Kz+Lw1⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤
- 可以看到, D H L 会与 w 相乘,从而实现位移
- M N O 会与 x y z 相乘,并加和在 w 分量上
- ⎣⎢⎡AEIBFJCGK⎦⎥⎤ 左上角这个矩阵完成旋转
- 主对角线完成缩放
齐次坐标的原理
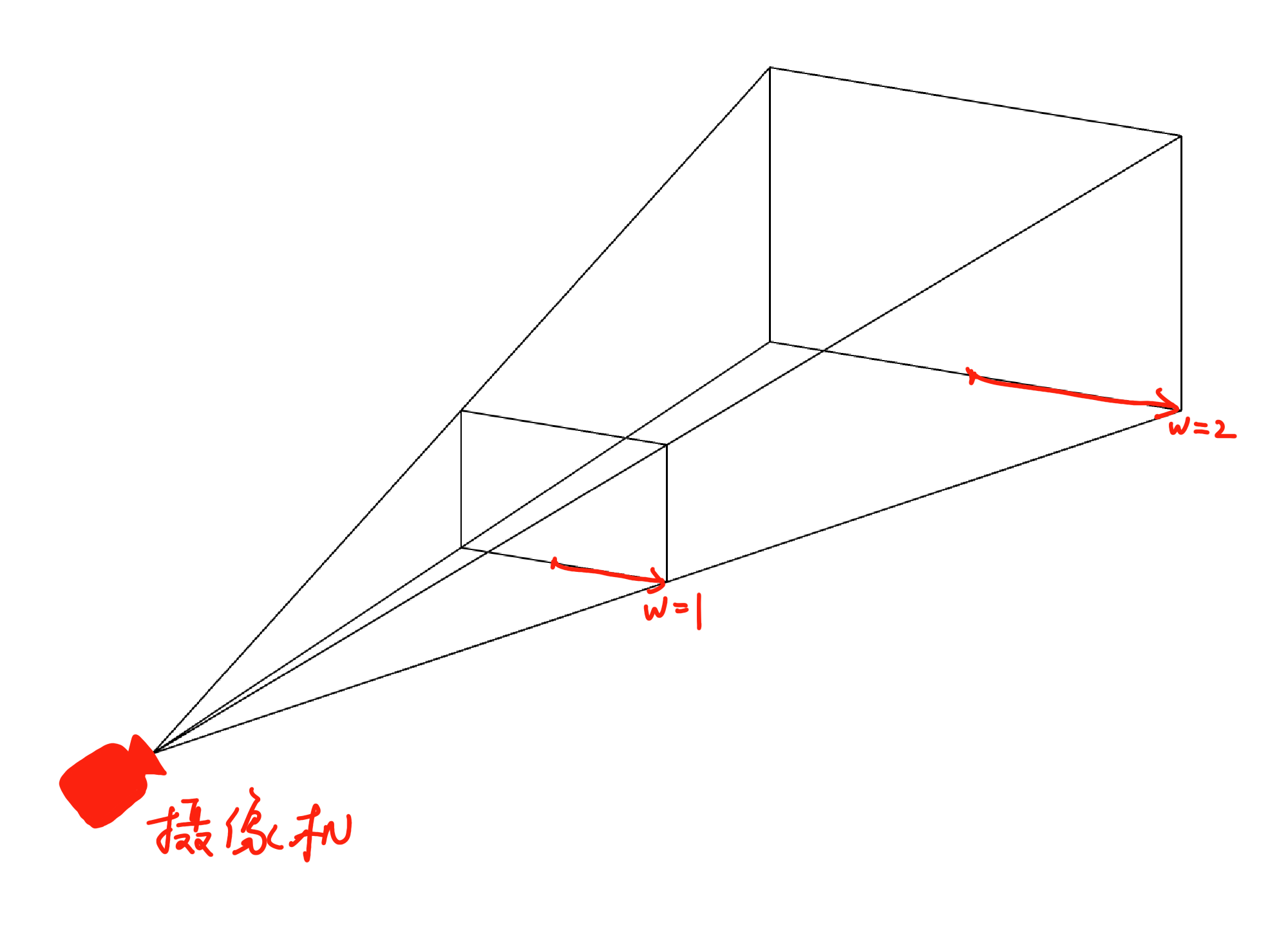
w 分量所表达的就是比例变换,可以看到图中的 w=1 的时候平移和 w=2 的位移距离完全不一样
将矩阵运算出来的向量分量除以 w ,并将 w 置为1(也可以减去 w 这个维度),这个过程叫做归一化
坐标 (x,y,z)的齐次坐标为(wx,wy,wz,w)
我们以三维物体投影到二维平面为例:
一个 (2,4,3) 坐标,映射到 z=5 的平面上
他的计算过程应该是这样的
先做归一化 (32,34,1) ,然后再翻到 z=5 的平面 (32×5,34×5,5)=(310,320,5) ,最终得到了坐标



