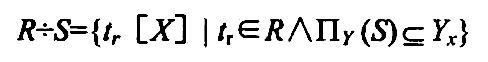传统的集合运算
1. 并
R∪S
2. 交
R∩S
3. 差
R−S
4. 笛卡尔积
R×S
4.1 域
域是一组具有相同数据类型的值的集合, 例如: { 李明, 张三 , 王五} , { 男, 女 } , { 计算机 , 旅游管理 }
4.2 笛卡尔积
笛卡尔积是域上的集合运算, 允许某些域上是相同的
按域的顺序, 每个域任取一个值, 列出所有的组合, 就是笛卡尔积
D1×D2×⋅⋅⋅Dn={(d1,d2⋅⋅⋅dn)∣di∈Di, i=1,2, ⋅⋅⋅ ,n}
| 姓名 |
性别 |
专业 |
| 李明 |
男 |
计算机 |
| 李明 |
男 |
旅游管理 |
| 李明 |
女 |
计算机 |
| 李明 |
女 |
旅游管理 |
| 张三 |
男 |
计算机 |
| 张三 |
男 |
旅游管理 |
| 张三 |
女 |
计算机 |
| 张三 |
女 |
旅游管理 |
| 王五 |
男 |
计算机 |
| 王五 |
男 |
旅游管理 |
| 王五 |
女 |
计算机 |
| 王五 |
女 |
旅游管理 |
专门的关系运算符
前置知识
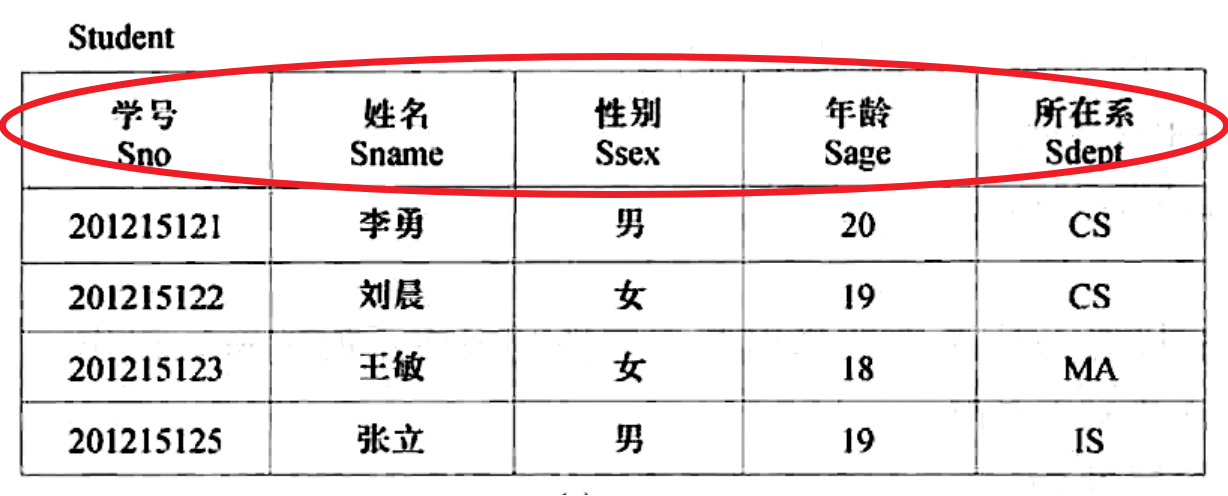
关系模式
表示一张表的首行信息,是一个关系的抽象,例如:关系模式:R(A1,A2,...,An),A1,A2,...,An 是属性抽象
比如下图表的第一行:
关系
一张表代表一个关系,n 目,表示 n 列,例如:Rn , 上面的图表就是一个 5 目关系
属性
表内的首行的每个元素叫属性,一个属性对应一列,从第二行开始,下面的都是属性的具体数值
例如: 属性集合 A={(Ai1,Ai2,...,Aik),i∈[1,n]}, i 是行数,k 是列数,这表示第 i 行的每列的分量集合,叫做属性组(属性列)。
A 表示取反,也就是除去第 i 行的其他属性组 ( 集合 ) , 其实就是集合取反
元组
表内的一行叫关系的一个元组
例如:t∈R,t[Ai] 表示 t 元组中的 Ai 分量,也就是属性 A 的第 i 行
Student 表的 元组一共有 4 个 ( 不包含第一行, 也就是不包含关系模式 )
t[Sname2]=刘晨
t[A]=(t[Ai1],t[Ai2],...,t[Aik]) 表示元组 t 在属性列 A 上各分量的集合
元组连接
{trts⌢ tr∈Rnts∈Sm}
成为元组连接,形成一个 n+m 列的元组,前 n 个分量为 R 中的一个 n 元组,也就是 n 列,前 m 个分量为 S 中的一个 m 元组,也就是 m 列。
其实就是把两个元组直接拼到一起
例如将李勇和刘晨这两个元组进行连接:

连接还有一些其他的形式: 等值连接, 非等值连接, 自然连接……后面会说到
象集
关系 R(X,Y) , X 和 Y 为属性组。当 t[X]=x 时,x 在 R 中的象集(images set)为:Yx={ t[Y] ∣ t∈R ,t[X]=x }
下图是 t[Y]=2 , y 在 R 中的象集:
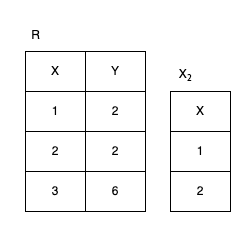
如果你看了后面的计算,那么象集你可以直接用选择加投影来计算象集,比如图中的就是先选择 Y=2 再做 x 的投影
选择
σF(R) 表示在 R 中选出符合条件 F 的元组(也就是行)
σF(R)=t∈R∧F(t)=′真′
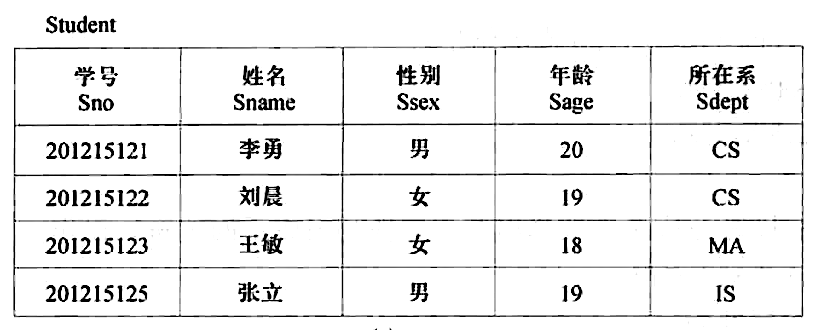
查询所在系为 IS 的学生,则 σSdept=CS(Student) 结果如图所示

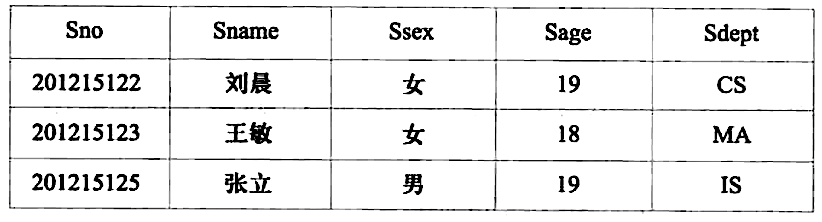
查询年龄小于 20 的学生,则 σSage<20(Student) 结果如图所示
投影
ΠA(R) 表示关系 R 上 A 的投影,是 R 中对应若干属性列组成新的关系 (A 是属性列) , 是只对应属性 A 的集合。
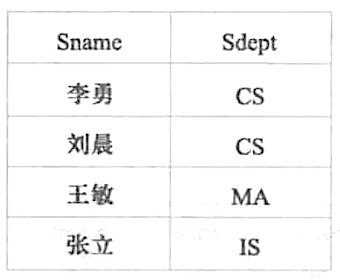
在 Student 中查询姓名与所在系的关系,ΠSname,Sdept(Student) 结果如图所示
连接
连接也称 θ 连接. 他是从两个关系的笛卡尔积中选取属性间满足一定条件的元组
R⋈AθBS={trts⌢ ∣ tr∈R∧ts∈S∧tr[A]θts[B]}
AθB 是条件, A 和 B 分别为 R 和 S 上列数相等且可比的属性组, θ 是比较运算符.
连接运算从 R 和 S 的笛卡尔积 R×S 中 , 选取 R 关系在 A 属性组上的值 与 S 关系在 B 属性组上的值 满足比较关系 θ 的元组
等值连接
θ 为 = 的连接运算称为等值连接
非等值连接、等值连接、自然连接
自然连接是一种特殊的等值连接。它要求两个关系中进行比较的分量必须是同名的属性组,并且在结果中把重复的属性列去掉。
如图就是非等值连接,等值连接,自然连接的对比
可以看到,
-
非等值连接是符合 C<E 的笛卡尔积元组,
-
R⋈R.B=S.BS 是符合 R.B=S.B 的等值连接,
-
自然连接要求进行比较的属性 ( 分量 ) 必须是同名的属性组, 并且在结果中把重复的属性组列去掉
也就是将同属性的两列合并成一列
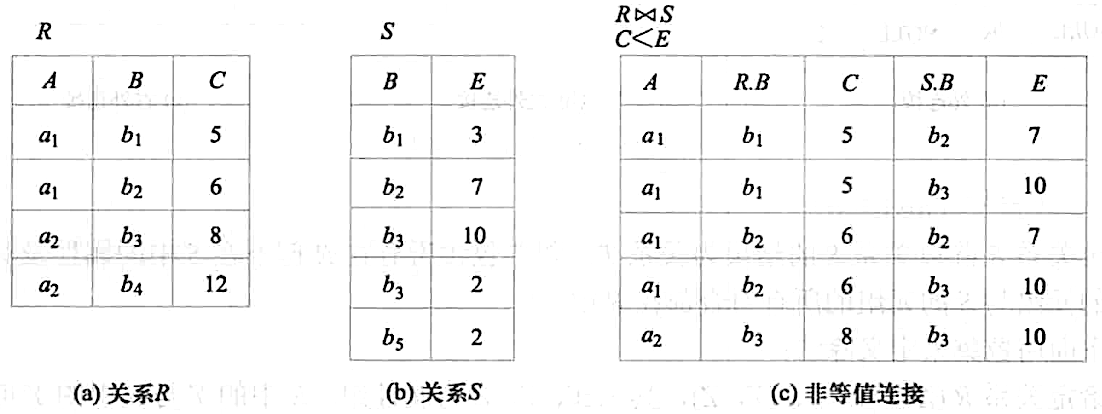
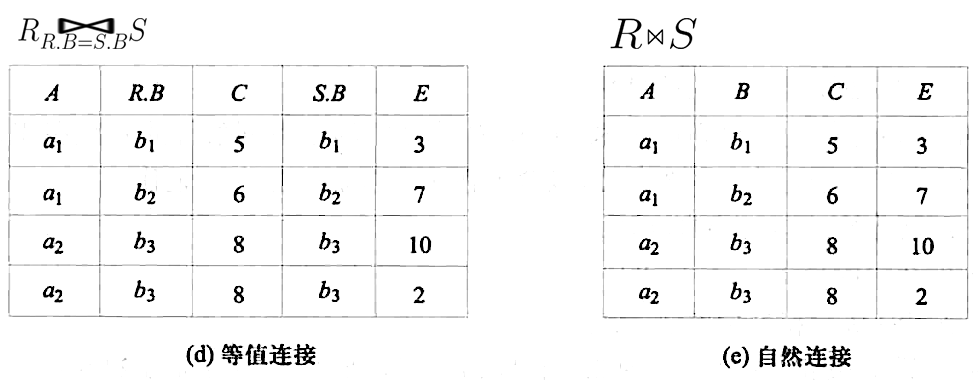
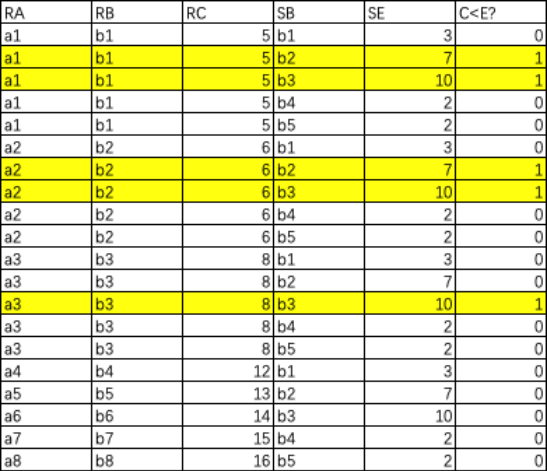
举一个 非等值连接 的计算过程 , 如图是笛卡尔积 , 黄色的是满足 C<E 的
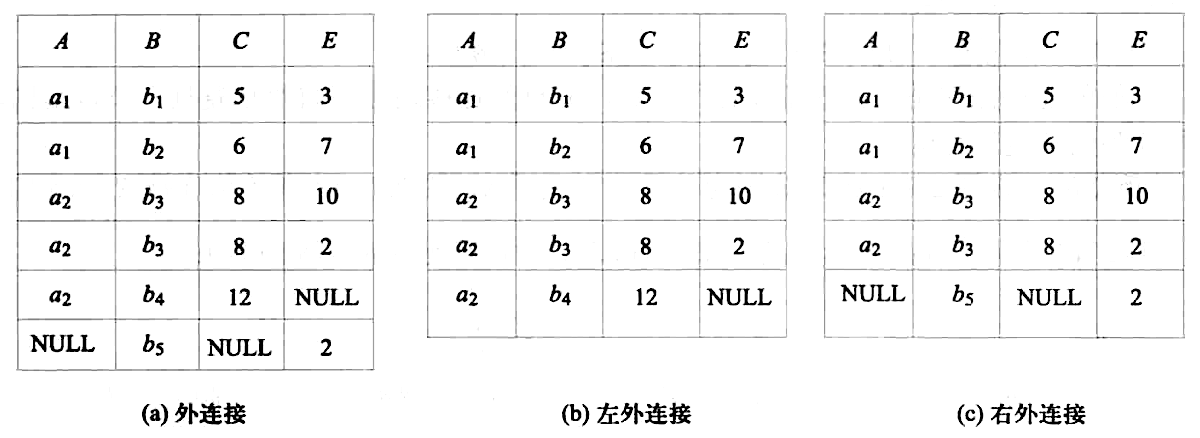
外连接
做自然连接的时候,会有一些不满足条件的元组被舍弃,叫 悬浮元组。
- R⋉⋊S,外连接是保留(不舍弃)悬浮元组的连接
- R⋉S,左外连接是保留左边关系的悬浮元组的连接
- R⋊S,右外连接是保留右边关系的悬浮元组的连接
在下图可以看到,
R 中 a2 b4 12 没有对应的 E 值,所以填 NULL
同样,S 中 b5 也没有对应的 A 和 E 值,也填 NULL
除运算
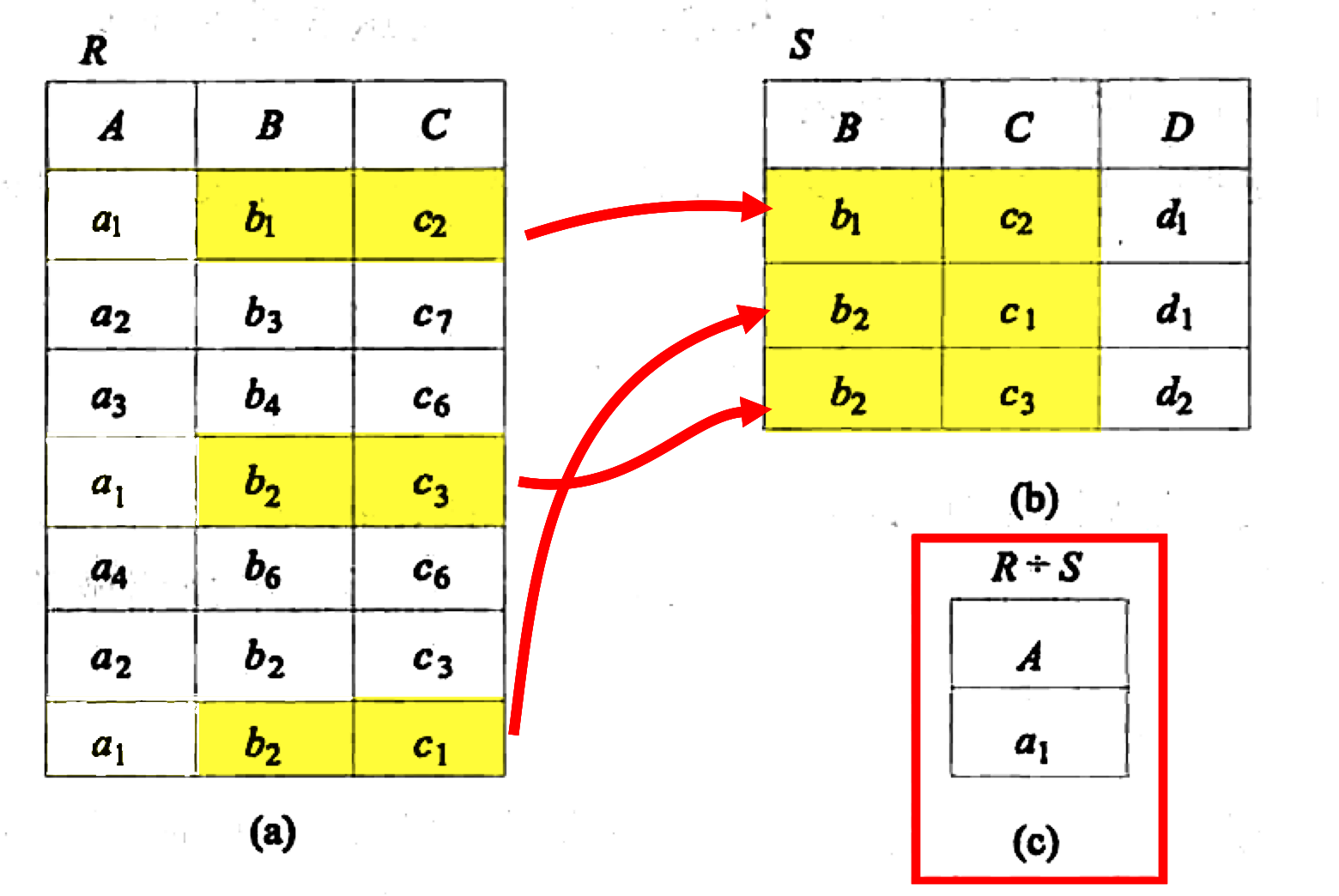
T=R÷S 表示 关系 T 是 关系 R 除以 关系 S 的结果(商)
T 包含所有在 R 但不在 S 中的属性及其值, 且 T 的元组与 S 的元组的所有都在 R 中, 也就是 S 和 T 的组合都是 R 的子集。(所以这个有排除的意思, 更像减法)
给定关系 R(X,Y) 和 S(Y,Z) , 其中 X,Y,Z 为属性组, R 中的 Y 和 S 中的 Y 可以有不同的属性名, 但必须出自相同的域集 ( 也就是有相同的类型 )
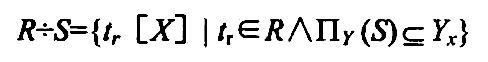
我们看这个式子,给定关系 R(X,Y) 和 S(Y,Z)
-
R÷S 的结果是一个集合, 集合里的元素是 tr[X] 也就是 属性 X 的一个分量
-
tr∈R 表示元组属于关系 R , 表示 新关系 T 是 R 的子集 ( 集合里的元素是元组 )
-
ΠY(S)⊆Yx 表示 关系 S 中的 Y 属性, 应该在 x 在 R 中的象集里
象集 Yx 是为了逐一比较, 不同 x 下的 Y 是否包含 S 中 Y 的投影
举例: 下图可以看到,只有 R 中的 a1 b1 c2,a1 b2 c3,a1 b2 c1
-
首先看,包含在 R 但是不包含在 S 的属性显然是属性 A,所以我们求解的答案肯定是一个 A 分量 的列
-
其次,求出 A 的所有值对应的象集,也就是 a1,a2,a3,a4 的象集
各象集
BCa1={(b1,c1),(b3,c7),(b2,c1)}
BCa2={(b3,c7),(b2,c3)}
BCa3={(b4,c6)}
BCa4={(b6,c6)}
-
求出 S 中 BC 的投影
ΠBC(S)={(b1,c2),(b2,c1),(b2,c3)}
-
然后确定包含关系,发现只有 a1 包含 S 中的 BC 所有组合
-
答案就是 a1